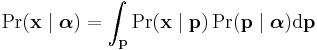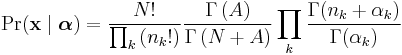Multivariate Pólya distribution
The multivariate Pólya distribution, named after George Pólya, also called the Dirichlet compound multinomial distribution, is a compound probability distribution, where a probability vector p is drawn from a Dirichlet distribution with parameter vector  , and a set of discrete samples is drawn from the categorical distribution with probability vector p. The compounding corresponds to a Polya urn scheme. In document classification, for example, the distribution is used to represent probabilities over word counts for different document types.
, and a set of discrete samples is drawn from the categorical distribution with probability vector p. The compounding corresponds to a Polya urn scheme. In document classification, for example, the distribution is used to represent probabilities over word counts for different document types.
Contents |
Probability mass function
We are doing N independent draws from a categorical distribution with K categories. Let x=(n1,n2,...,nK) denote the vector of counts, where nk is the number of times category k was drawn. If the parameter of the categorical distribution is given as p=(p1,p2,...,pK), where 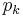 is the probability to draw value k, the probability distribution for counts, P(x|p) is given by the associated multinomial distribution with parameter p. But now p is not given, but instead considered drawn from a Dirichlet distribution with parameter vector
is the probability to draw value k, the probability distribution for counts, P(x|p) is given by the associated multinomial distribution with parameter p. But now p is not given, but instead considered drawn from a Dirichlet distribution with parameter vector 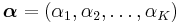 . The resulting compound distribution is obtained by integrating out p:
. The resulting compound distribution is obtained by integrating out p:
which results in the following explicit formula:
where 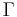 is the gamma function, with
is the gamma function, with
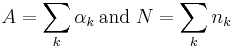 .
.
Another form
The probability mass function may be written more compactly in terms of the beta function, as follows:
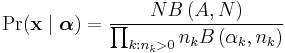
where  is the beta function.
is the beta function.
Related distributions
The one-dimensional version of the multivariate Pólya distribution is known as the Beta-binomial distribution.
Uses
The multivariate Pólya distribution is used in automated document classification and clustering, genetics, economy, combat modeling, and quantitative marketing.
See also
- Beta-binomial distribution
- Chinese restaurant process
- Dirichlet process
- Generalized Dirichlet distribution
References
- Elkan, C. (2006) Clustering documents with an exponential-family approximation of the Dirichlet compound multinomial distribution. ICML, 289-296
- Kvam, P. and Day, D. (2001) The multivariate Polya distribution in combat modeling. Naval Research Logistics, 48, 1-17
- Madsen, RE., Kauchak, D. and Elkan, C. (2005) Modeling Word Burstiness Using the Dirichlet Distribution. ICML, 545-552
- Minka, T. (2003) Estimating a Dirichlet distribution. Technical report Microsoft Research. Includes Matlab code for fitting distributions to data.
- Wagner, U. and Taudes, A. (1986) A Multivariate Polya Model of Brand Choice and Purchase Incidence. Marketing Science, 5(3), 219-244.